Estudio sobre la eficiencia y la resistencia a la temperatura del cristal PPLN chirriado en un experimento de duplicación de frecuencia de 1064 nm - 02

2. Análisis teórico

2.1 Resistencia a la temperatura

La robustez a la temperatura se refiere a la estabilidad del cristal de frecuencia duplicada con respecto a la temperatura. Específicamente, cuando la temperatura fluctúa, la potencia de la luz de frecuencia duplicada no se verá muy afectada. La influencia de la temperatura en el proceso de duplicación de frecuencia proviene principalmente de la influencia en el desajuste de fases. Durante el proceso de duplicación de frecuencia, en el caso de una pequeña aproximación de señal, la potencia de la luz de frecuencia duplicada se puede expresar como:

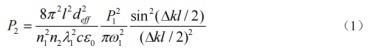
Enecuación 1,yoes la longitud del cristal de duplicación de frecuencia;d_effes el coeficiente no lineal efectivo;Ces la velocidad de la luz en el vacío;ε₀es la constante dieléctrica del vacío;PAG_i,λ_i,norte_i, yω_isontLa potencia, longitud de onda, índice de refracción y radio de cintura del haz delFfrecuencia fundamentalhazy frecuencia-dudarcondujohazrespectivamente. tél subíndicei=1, 2 corresponden a la frecuencia fundamentalhazy la frecuencia se duplicóhazrespectivamente; la cantidad de desajuste de fase Δk=k₂-2k₁,en que onda vsectork_i=(norte_i2π)/λ_i. Se puede ver en la ecuación1 que sólo cuando se cumple la condición de coincidencia de fases, es decir, cuando Δk= 0, se puede obtener la máxima potencia óptica duplicada en frecuencia. En el proceso de coincidencia de casi fases, dado que la dirección de polarización espontánea del cristal no lineal se cambia artificial y periódicamente, el período de polarizaciónΛintroducirá el vector reticular inversoGRAMO_metro. La relación entre el vector reticular inverso y el período de polarización es:

GRAMO_metro=metro(2π/Λ) (2)

W.aquímetrorepresenta elnúmerometroordenar la coincidencia cuasi-fase.Entoncesel desajuste de fases en el proceso de duplicación de frecuencia se puede reescribir como:

Δk'=k₂-2k₁-GRAMO_metro(3)

Se sabe de laSecuación de elmeier:wCuando la temperatura cambia, el índice de refracciónnorte_itambién se verá afectado, lo que a su vez afecta el desajuste de fase Δk. Desde el período de polarización del PPLN(www.wisoptic.com)es un período único y el vector recíproco introducido es un valor fijo, coincidencia de fase Δk'= 0 solo se puede lograr en longitudes de onda específicas y condiciones de temperatura específicas.Por lo tantopodemos saber que el punto clave para lograr robustez a la temperatura es expandir el ancho de banda de ganancia del cristal polarizado para que el vector reticular inverso pueda cubrir un cierto rango.yel desajuste de fases aún puede satisfacer Δk'= 0 cuando cambia la temperatura.IEn otras palabras, la resistencia a la temperatura está relacionada con el ancho de banda de ganancia del cristal. Cuanto mayor sea el ancho de banda de ganancia, mejor será la robustez térmica del cristal. El período de polarización de PPLN se puede expresar como una función de la posición.como sigue:

En la fórmula,D_gramoes el grado de chirrido del cristal CPPLN(www.wisoptic.com), yΛ₀es el período inicial de CPPLN. Se puede ver desdemiCuación 4 que cubre el período de polarización de CPPLNΛ₁= 2πΛ₀yΛ₂=Λ₀/[(1+D_gramoΛ₀yo)/2π]. Y cambia continuamente dentro de este rango, es decir, el CPPLN de esta estructura puede proporcionar un vector de red inverso que cambia continuamente dentro de un cierto rango. Cuando el desajuste de fase k cambia dentro de este rango debido a la temperatura, el vector reticular inverso de CPPLN compensará perfectamente su valor cambiante para garantizarΔk' = 0, es decir, la eficiencia de conversión de la luz de frecuencia duplicada se puede mantener en un nivel muy alto dentro de un cierto rango de temperatura. Sin embargo, cabe señalar que cuanto mayor sea el rango del período de polarización de CPPLN no es mejor, porque el aumento del chirrido conducirá a la reducción del coeficiente no lineal efectivo. Por lo tanto, en el proceso de producción real, se debe lograr un equilibrio entre la resistencia a la temperatura y la mayor eficiencia de multiplicación de frecuencia.